비율검정

단일 비율

binom.test

• 성공 확률에 대한 간단한 귀무 가설 테스트
• binom.test(x, n, p=0.5, alternative = c("two.sided", "less", "greater"), conf.level = 0.95)

x	성공횟수
n	시행횟수
p	가정한 확률
alternative	대체 가설
conf.level	반환된 신뢰구간에 대한 신뢰수준

binom.test(67,120)

---

두 비율의 차이

prop.test

• 여러그룹의 비율이 같거나 특정값이 같은지 비교하는 test
• prop.test(x, n, p=NULL, alternative = c("two.sided", "less", "greater"), conf.level = 0.95, correct = TRUE)

x	성공횟수
n	시행횟수
p	가정한 확률
alternative	대립 가설
conf.level	반환된 신뢰구간에 대한 신뢰수준
correct	연속성 보정을 적용해야하는지 여부를 나타내는 논리

 

• 홍보하기 전과 홍보하고 난 뒤 제품에 대한 인지도를 비교

	전	후
인지O	60	130
인지X	90	230
합	150	360

prop.test(c(60,130),c(150,250),alternative="greater")

• 귀무가설( p-value > 0.05 )

1. A = B
2. A<=B
3. A>=B

• 대립가설( p-value < 0.05 )

1. A!=B (diffrent)
2. A>B  (greater)
3. A<B  (less)

p-value값이 0.05를 넘기므로 귀무가설이 채택되고 greater 조건에 의해 전 비율보다 후 비율이 크므로, 홍보가 제대로 됬다고 볼 수 있다.

---

적합도 검정

• 데이터의 분포가 특정 분포함수와 얼마나 잘 맞는지 test
• chisq.test(x, y=NULL, correct = TRUE, p=rep(1/length(x), length(x)), rescale.p=FALSE, simulate.p.value=FALSE, B=2000)

인수	정의
x	숫자vector, 행렬x or 행렬y
y	숫자vector, x가 행렬이면 무시, x가 인수이면 같은길이
correct	연속성 보정을 적용할지 여부, simulater.p.value가 TRUE이면 실행되지 않음
p	동일한 x 길이의 확률vector, 음수면 오류
rescale.p	TRUE이면 p=1, FALSE일 때 p가 1이되면 오류
simulate.p.value	p-value를 계산할지 여부를 결정
B	반복횟수 지정

x=c(30,20,35,15)
chisq.test(x)

p-value값이 0.05보다 작으므로 귀무가설을 기각하고, 대립가설을 채택하여 데이터의 분포가 적합하지 않다.

---

독립성 검정

• 서로 다른 요인들에 의해 분할되어 있는 경우 그 요인들이 관찰값에 영향을 주는지 test

chisq.test(matrix(c(18,12,6,14,19,16,12,3), ncol=4))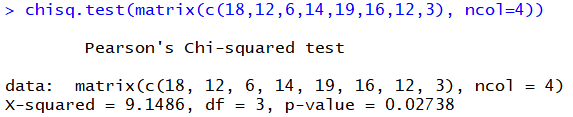

p-value값이 0.05보다 작다.

따라서 서로 독립적이지 않다.